링크 : https://www.acmicpc.net/problem/1854
문제 설명 :
봄캠프를 마친 김진영 조교는 여러 도시를 돌며 여행을 다닐 계획이다. 그런데 김 조교는, '느림의 미학'을 중요시하는 사람이라 항상 최단경로로만 이동하는 것은 별로 좋아하지 않는다. 하지만 너무 시간이 오래 걸리는 경로도 그리 매력적인 것만은 아니어서, 적당한 타협안인 'k번째 최단경로'를 구하길 원한다. 그를 돕기 위한 프로그램을 작성해 보자.
입력 :
첫째 줄에 n, m, k가 주어진다. (1 ≤ n ≤ 1000, 0 ≤ m ≤ 2000000, 1 ≤ k ≤ 100) n과 m은 각각 김 조교가 여행을 고려하고 있는 도시들의 개수와, 도시 간에 존재하는 도로의 수이다.
이어지는 m개의 줄에는 각각 도로의 정보를 제공하는 세 개의 정수 a, b, c가 포함되어 있다. 이것은 a번 도시에서 b번 도시로 갈 때는 c의 시간이 걸린다는 의미이다. (1 ≤ a, b ≤ n. 1 ≤ c ≤ 1000)
도시의 번호는 1번부터 n번까지 연속하여 붙어 있으며, 1번 도시는 시작도시이다.
출력 :
n개의 줄을 출력한다. i번째 줄에 1번 도시에서 i번 도시로 가는 k번째 최단경로의 소요시간을 출력한다.
경로의 소요시간은 경로 위에 있는 도로들을 따라 이동하는데 필요한 시간들의 합이다. i번 도시에서 i번 도시로 가는 최단경로는 0이지만, 일반적인 k번째 최단경로는 0이 아닐 수 있음에 유의한다. 또, k번째 최단경로가 존재하지 않으면 -1을 출력한다. 최단경로에 같은 정점이 여러 번 포함되어도 된다.
예제 입력 :
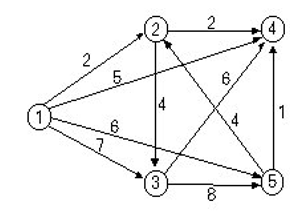
5 10 2
1 2 2
1 3 7
1 4 5
1 5 6
2 4 2
2 3 4
3 4 6
3 5 8
5 2 4
5 4 1
예제 출력 :
-1
10
7
5
14
접근법 :
1) 어떻게 풀 것인가?
경로 중 음수간선이 없는 경우, 최단경로를 찾는 알고리즘은 다익스트라가 있다.
PQ를 활용할 경우 시간복잡도도 우수한 편이어서 O(ElogV) 이 문제와 같이 간선 수가
2,000,000과 같이 비교적 클때 활용하기 좋다.
그런데, 다익스트라는 최단거리를 찾는 알고리즘인데, 이 문제에서 요구하는 것은 K번째 최단거리이다.
심지어 K는 100까지 가능하다.
K가 제법 크다는 점에서 여기서 단순 if 문을 활용한 DP점화식이나,
다차원 배열로 하는 것 보다 자료구조를 활용하면 빠른 답을 구할 수 있다고 판단했다.
일반적인 다익스트라에서 int [ ] dist를 활용하는것과 달리 PriorityQueue<Integer>[ ] dist를 만들어
MaxHeap으로 하고 그 크기를 K로 한정짓는다면,
dist.peek( ); 을 했을때 바로 K번째 최단거리를 알 수 있게 된다.
PQ dist를 활용한 k번째 최단경로를 찾는 다익스트라 함수는 아래와 같다.
static void kthDijkstra(int start) {
// 1. 일반 다익스트라처럼 출발점 비용 0 넣고 시작
PriorityQueue<edge> pq = new PriorityQueue<edge>();
pq.add(new edge(start,0));
dist[start].add(0);
// 2. pq를 비울때까지 다익스트라 진행 (K번째 경로를 확인해야하므로 모두 확인)
while(!pq.isEmpty()) {
edge now = pq.poll();
int len = adjList[now.target].size();
for (int i = 0; i<len; i++) {
edge next = (Main.edge) adjList[now.target].get(i);
// 2-1. 저장된 최단비용이 K개 이하인 경우 PQ에 넣기 -> 넣으면 알아서 정렬
if (dist[next.target].size() < K) {
// minHaep을 maxHeap으로 바꾸기 위해 -1을 곱해서 dist pq에 넣기
dist[next.target].add((now.cost + next.cost)* -1 );
// 일반 다익스트라와 동일하게 최솟값이 경신되었으므로 pq에 넣기
pq.add(new edge(next.target, now.cost + next.cost));
}
// 2-2. 저장된 비용이 K개이므로, dist MAX 값과 비교해서 작은 값을 dist PQ에 갱신
else if ((dist[next.target].peek())*-1 > (now.cost + next.cost)) {
dist[next.target].poll(); // 뽑기
// minHaep을 maxHeap으로 바꾸기 위해 -1을 곱해서 dist pq에 넣기
dist[next.target].add((now.cost+next.cost)*-1);
// 일반 다익스트라와 동일하게 최솟값이 경신되었으므로 pq에 넣기
pq.add(new edge(next.target, now.cost + next.cost));
}
}
}
}
자세한 내용은 아래 코드 참고.
이 문제를 풀기 전에 백준 1753 최단경로 먼저 추천 https://subbak2.tistory.com/55
[BOJ 백준] 최단경로(1753) Java
링크 : https://www.acmicpc.net/problem/1753 문제 설명 : 더보기 방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 1
subbak2.tistory.com
2) 시간복잡도
일반적으로 목적지만 도착하면 끝나는 다익스트라 O(ElogV)와 달리
PQ가 완전히 빌때까지 다익스트라를 수행하지만 N이 1,000으로 비교적 작은편이라 큰 무리는 없다.
(Java 기준 - 1,132ms)
3) 공간복잡도
ArrayList로 인접리스트를 구현한다면,
간선이 200만개로 적지 않지만, N이 1,000이고 다차원 배열이 없어 무리없다.
4) 풀면서 놓쳤던점
특별히 없음.
5) 이 문제를 통해 얻어갈 것
K번째 최단경로 찾는 다익스트라 코드 작성법
Java 코드 :
import java.io.*;
import java.util.*;
// 1854 K번째 최단경로 찾기
public class Main {
static int N, M, K; // N : 도시 수, M : 도로 수, K : K번째 경로
static ArrayList[] adjList; // 인접리스트
static PriorityQueue<Integer>[] dist; // dist[i] i번째 최단경로 - PQ로 K개 까지 저장
static class edge implements Comparable<edge>{
int target, cost;
public edge(int target, int cost) {
this.target = target;
this.cost = cost;
}
@Override // 사전순 출력
public int compareTo(Main.edge o) {
return this.cost - o.cost;
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
// 1. 입력 & 변수 준비
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
// 1-1. 인접리스트, 거리배열 초기화
adjList = new ArrayList[N+1];
dist = new PriorityQueue[N+1];
for (int i = 1; i<=N; i++) {
adjList[i] = new ArrayList<Integer>();
dist[i] = new PriorityQueue<Integer>(K); // K개만큼만 할당
}
// 1-2. 단방향 간선 입력
int a, b, c;
for (int i = 1; i<= M; i++) {
st = new StringTokenizer(br.readLine());
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
adjList[a].add(new edge(b,c));
}
// 2. K번째 최단경로를 찾는 다익스트라
kthDijkstra(1);
// 3. 출력
StringBuilder sb = new StringBuilder ();
for (int i = 1; i<=N; i++) {
// K번째 최단경로 존재하는 경우
if (dist[i].size() == K) sb.append((dist[i].peek() * -1)+"\n");
// 존재하지 않는 경우
else sb.append("-1\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static void kthDijkstra(int start) {
// 1. 일반 다익스트라처럼 출발점 비용 0 넣고 시작
PriorityQueue<edge> pq = new PriorityQueue<edge>();
pq.add(new edge(start,0));
dist[start].add(0);
// 2. pq를 비울때까지 다익스트라 진행 (K번째 경로를 확인해야하므로 모두 확인)
while(!pq.isEmpty()) {
edge now = pq.poll();
int len = adjList[now.target].size();
for (int i = 0; i<len; i++) {
edge next = (Main.edge) adjList[now.target].get(i);
// 2-1. 저장된 최단비용이 K개 이하인 경우 PQ에 넣기 -> 넣으면 알아서 정렬
if (dist[next.target].size() < K) {
// minHaep을 maxHeap으로 바꾸기 위해 -1을 곱해서 dist pq에 넣기
dist[next.target].add((now.cost + next.cost)* -1 );
// 일반 다익스트라와 동일하게 최솟값이 경신되었으므로 pq에 넣기
pq.add(new edge(next.target, now.cost + next.cost));
}
// 2-2. 저장된 비용이 K개이므로, dist MAX 값과 비교해서 작은 값을 dist PQ에 갱신
else if ((dist[next.target].peek())*-1 > (now.cost + next.cost)) {
dist[next.target].poll(); // 뽑기
// minHaep을 maxHeap으로 바꾸기 위해 -1을 곱해서 dist pq에 넣기
dist[next.target].add((now.cost+next.cost)*-1);
// 일반 다익스트라와 동일하게 최솟값이 경신되었으므로 pq에 넣기
pq.add(new edge(next.target, now.cost + next.cost));
}
}
}
}
}'알고리즘 Algorithm > BOJ 백준 (초급~중급)' 카테고리의 다른 글
| [BOJ 백준] 구간 합 구하기 5(11660) Java (0) | 2021.07.27 |
|---|---|
| [BOJ 백준] 구간 합 구하기 4(11659) Java (0) | 2021.07.27 |
| [BOJ 백준] 단절선(11400) Java (0) | 2021.07.27 |
| [BOJ 백준] 도로 네트워크(3176) Java (0) | 2021.07.26 |
| [BOJ 백준] LCA 2(11438) Java (0) | 2021.07.26 |


