링크 : https://www.acmicpc.net/problem/2618
문제 설명 :
어떤 도시의 중심가는 N개의 동서방향 도로와 N개의 남북방향 도로로 구성되어 있다.
모든 도로에는 도로 번호가 있으며 남북방향 도로는 왼쪽부터 1에서 시작하여 N까지 번호가 할당되어 있고 동서방향 도로는 위부터 1에서 시작하여 N까지 번호가 할당되어 있다. 또한 동서방향 도로 사이의 거리와 남 북방향 도로 사이의 거리는 모두 1이다. 동서방향 도로와 남북방향 도로가 교차하는 교차로의 위치는 두 도로의 번호의 쌍인 (동서방향 도로 번호, 남북방향 도로 번호)로 나타낸다. N이 6인 경우의 예를 들면 다음과 같다.
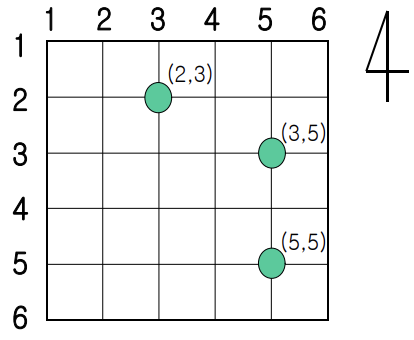
이 도시에는 두 대의 경찰차가 있으며 두 차를 경찰차1과 경찰차2로 부른다. 처음에는 항상 경찰차1은 (1, 1)의 위치에 있고 경찰차2는 (N, N)의 위치에 있다. 경찰 본부에서는 처리할 사건이 있으면 그 사건이 발생된 위치를 두 대의 경찰차 중 하나에 알려 주고, 연락 받은 경찰차는 그 위치로 가장 빠른 길을 통해 이동하여 사건을 처리한다. (하나의 사건은 한 대의 경찰차가 처리한다.) 그리고 사건을 처리 한 경찰차는 경찰 본부로부터 다음 연락이 올 때까지 처리한 사건이 발생한 위치에서 기다린다. 경찰 본부에서는 사건이 발생한 순서대로 두 대의 경찰차에 맡기려고 한다. 처리해야 될 사건들은 항상 교차로에서 발생하며 경찰 본부에서는 이러한 사건들을 나누어 두 대의 경찰차에 맡기되, 두 대의 경찰차들이 이동하는 거리의 합을 최소화 하도록 사건을 맡기려고 한다.
예를 들어 앞의 그림처럼 N=6인 경우, 처리해야 하는 사건들이 3개 있고 그 사건들이 발생된 위치 를 순서대로 (3, 5), (5, 5), (2, 3)이라고 하자. (3, 5)의 사건을 경찰차2에 맡기고 (5, 5)의 사건도 경찰차2에 맡기며, (2, 3)의 사건을 경찰차1에 맡기면 두 차가 이동한 거리의 합은 4 + 2 + 3 = 9가 되 고, 더 이상 줄일 수는 없다.
처리해야 할 사건들이 순서대로 주어질 때, 두 대의 경찰차가 이동하는 거리의 합을 최소화 하도록 사건들을 맡기는 프로그램을 작성하시오.
입력 :
첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄까지 사건이 발생된 위치가 한 줄에 하나씩 주어진다. 경찰차들은 이 사건들을 주어진 순서대로 처리해야 한다. 각 위치는 동서방향 도로 번호를 나타내는 정수와 남북방향 도로 번호를 나타내는 정수로 주어지며 두 정수 사이에는 빈칸이 하나 있다. 두 사건이 발생한 위치가 같을 수 있다.
출력 :
첫째 줄에 두 경찰차가 이동한 총 거리를 출력한다. 둘째 줄부터 시작하여 (i+1)번째 줄에 i(1 ≤ i ≤ W)번째 사건이 맡겨진 경찰차 번호 1 또는 2를 출력한다.
예제 입력 :
6
3
3 5
5 5
2 3
예제 출력 :
9
2
2
1
접근법 :
1) 어떻게 풀 것인가?
DP 배열 정의시 dp[i][j][k][l] 처럼 4차원으로 선언해 경찰 2명의 좌표를 기록할 경우 시간초과가 예상된다.
약간의 발상의 전환이 필요한것 같아 아래처럼 dp 배열을 정의했다.
dp[i][j] = 1번 경찰차가 i번 사건을 처리했고, 2번 경찰차가 j번 사건을 처리했을때 최소비용
전체 비용을 구하는것 외에 한 번 더 길을 찾아야하는 다소 까다로운 문제였다.
전체 코드는 아래 참고.
2) 시간복잡도
최악의 경우 N^2 예상되나, DP 가지치기로 무리 없이 통과됨.
(Java 기준 - 280ms)
3) 공간복잡도
W = 1,000으로 크지 않아 고려하지 않음.
4) 풀면서 놓쳤던점
특별히 없음.
5) 이 문제를 통해 얻어갈 것
DP Ad-hoc적 사고. 어떻게 dp 배열을 정의할 것인가.
Java 코드 :
import java.io.*;
import java.util.*;
// 2618 경찰차
public class Main {
static class point {
int x, y;
public point(int x, int y) {
this.x = x;
this.y = y;
}
}
static int N, W;
static point[] event;
static int[][] dp; // dp[i][j] = 1번 경찰차가 i번 사건을 처리했고, 2번 경찰차가 j번 사건을 처리했을때 최소비용
static StringBuilder sb;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(br.readLine());
W = Integer.parseInt(br.readLine());
event = new point[W + 1];
StringTokenizer st;
int y, x;
for (int i = 1; i <= W; i++) {
st = new StringTokenizer(br.readLine());
x = Integer.parseInt(st.nextToken());
y = Integer.parseInt(st.nextToken());
event[i] = new point(x, y);
}
dp = new int[W + 1][W + 1];
for (int i = 0; i <= W; i++) {
for (int j = 0; j <= W; j++) {
dp[i][j] = -1;
}
}
sb = new StringBuilder();
sb.append(getTotDistance(0, 0) + "\n");
getPath(0, 0);
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static int getTotDistance(int police1, int police2) {
// 1. 탈출조건
if (police1 == W || police2 == W) {
return 0;
}
// 2. 이미 계산한 dp면 가지치기
if (dp[police1][police2] != -1) {
return dp[police1][police2];
}
// 다음 사건 번호
int next = Math.max(police1, police2) + 1;
int dist1, dist2;
// 경찰 1의 지금까지의 거리
if (police1 == 0) {
dist1 = getDist(1, 1, event[next].x, event[next].y);
} else {
dist1 = getDist(event[police1].x, event[police1].y, event[next].x, event[next].y);
}
// 경찰 2의 지금까지의 거리
if (police2 == 0) {
dist2 = getDist(N, N, event[next].x, event[next].y);
} else {
dist2 = getDist(event[police2].x, event[police2].y, event[next].x, event[next].y);
}
// result1 : 경찰1이 문제 해결한 경우
int result1 = dist1 + getTotDistance(next, police2);
// result2 : 경찰2가 문제 해결한 경우
int result2 = dist2 + getTotDistance(police1, next);
// 최솟값
return dp[police1][police2] = Math.min(result1, result2);
}
static void getPath(int police1, int police2) {
if (police1 == W || police2 == W)
return;
int next = Math.max(police1, police2) + 1;
int dist1, dist2;
if (police1 == 0) {
dist1 = getDist(1, 1, event[next].x, event[next].y);
} else {
dist1 = getDist(event[police1].x, event[police1].y, event[next].x, event[next].y);
}
if (police2 == 0) {
dist2 = getDist(N, N, event[next].x, event[next].y);
} else {
dist2 = getDist(event[police2].x, event[police2].y, event[next].x, event[next].y);
}
if (dp[next][police2] + dist1 < dp[police1][next] + dist2) {
sb.append("1\n");
getPath(next, police2);
} else {
sb.append("2\n");
getPath(police1, next);
}
}
static int getDist(int x1, int y1, int x2, int y2) {
return Math.abs(x2 - x1) + Math.abs(y2 - y1);
}
}'알고리즘 Algorithm > BOJ 백준 (초급~중급)' 카테고리의 다른 글
| [BOJ 백준] 두 번째로 작은 스패닝 트리(1626) Java (0) | 2021.07.30 |
|---|---|
| [BOJ 백준] 공장 (7578) Java (0) | 2021.07.30 |
| [BOJ 백준] 케이크 자르기2 (10714) Java (0) | 2021.07.30 |
| [BOJ 백준] 발전소 (1102) Java (0) | 2021.07.30 |
| [BOJ 백준] 외판원 순회 (2098) Java, C (0) | 2021.07.30 |


