[BOJ 백준] LCS 2 (9252) Java

링크 : https://www.acmicpc.net/problem/9252

 

문제 설명 : 

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

 

입력 :

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

 

출력 : 

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.

LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.

 

예제 입력 : 

ACAYKP

CAPCAK

 

예제 출력 : 

4

ACAK

 

 

접근법 : 

1) 어떻게 풀 것인가?

LCS (최장 공통 부분 수열)의 공통 문자열 출력하는 문제이다.

 

위 그림은 예제로 주어진

ACAYKP와

CAPCAK를 비교했을때

ACAK라는 LCS를 찾는 과정을 나타낸 표이다.

 

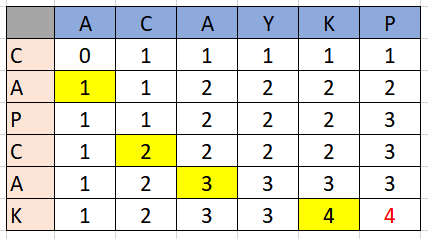
여기서 공통된 부분은 사선↘ 형태로 진행이 되며, 특이점은 공통 부분 문자열 문제와 달리 

칸을 건너뛸 수 있다는 점이다. 

 

이를 코드로 구현하면 된다.

 

아래 블로그보다 잘 설명할 자신이 없어서 자세한 내용은 링크로 대체

https://velog.io/@emplam27/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-LCS-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Longest-Common-Substring%EC%99%80-Longest-Common-Subsequence

[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence

 

작성한 코드는 아래 참고.

 

2) 시간복잡도

O(N^2)이나 N = 1,000으로 여유 있음

(Java 기준 -  168ms)

 

3) 공간복잡도

N(1,000)이 크지 않아 N^2으로도 충분함.

 

4) 풀면서 놓쳤던점

N, M 문자열 길이를 잘못잼. 

 

5) 이 문제를 통해 얻어갈 것

분할정복 코드 작성법

 

Java 코드 : 

import java.io.*;
import java.util.*;

// 9252 LCS2
public class Main {

	static int N, M;
	static String inputA, inputB;
	static int[][] dp;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		// 1. 입력받기
		inputA = br.readLine();
		inputB = br.readLine();
		N = inputA.length();
		M = inputB.length();

		// 2. 길이 구하기
		int ans = getLCSLength();

		// 3. 문자열 구하기
		StringBuilder sb = new StringBuilder();
		while ( N != 0 && M != 0) {
			if (inputA.charAt(N - 1) == inputB.charAt(M - 1)) {
				sb.insert(0, inputA.charAt(N - 1));
				N--;
				M--;
			} else if (dp[N][M] == dp[N - 1][M]) {
				N--;
			} else if (dp[N][M] == dp[N][M - 1]) {
				M--;
			}
		}
		// LCS 문자열 길이 출력
		bw.write(ans + "\n" + sb.toString());

		bw.flush();
		bw.close();
		br.close();
	}

	static int getLCSLength() {
		dp = new int[N+1][M+1];
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= M; j++) {
				// 2-1. 같으면 추가
				if (inputA.charAt(i-1) == inputB.charAt(j-1)) {
					dp[i][j] = dp[i - 1][j - 1] + 1;
				}
				// 2-2. 다르면
				else {
					dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
				}
			}
		}
		return dp[N][M];
	}

}