링크 : www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄��
www.acmicpc.net
문제 설명 :
어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.
입력 :
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1번째 줄까지 세 개의 정수 a, b, c가 주어지는데, a가 1인 경우 b번째 수를 c로 바꾸고 a가 2인 경우에는 b번째 수부터 c번째 수까지의 합을 구하여 출력하면 된다.
입력으로 주어지는 모든 수는 -2^63보다 크거나 같고, 2^63-1보다 작거나 같은 정수이다.
출력 :
첫째 줄부터 K줄에 걸쳐 구한 구간의 합을 출력한다. 단, 정답은 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
예제 입력 :
5 2 2
1
2
3
4
5
1 3 6
2 2 5
1 5 2
2 3 5
예제 출력 :
17
12
접근법 :
1) 어떻게 풀 것인가?
1,00,000개의 숫자가 주어지고, 10,000번 해당 숫자를 수정할 수 있으며, 10,000번 특정 구간에 대한 합을 물어본다.
숫자를 수정하는 상황과 구간 합을 물어보는 상황은 순서가 섞일 수 있다.
즉, 온라인으로 변화하는 값들의 합을 구해야한다, 온라인쿼리.
(반대개념 : 오프라인 쿼리 - 값이 변화하지 않는 상태에서 특정 질의를 수행)
가장 쉬운 방법은 배열에 100만개의 숫자를 받아놓고,
수정할때 그 숫자를 수정하고,
더할때 범위만큼 더하는 것이다.
그런데 이렇게 할 경우 최악의 경우 10,000번 모두 1~N까지 합 구하기가 나와버릴 경우
O(N*K)라는 100억의 시간복잡도가 나와 시간초과가 발생한다.
따라서 특정 구간의 합을 미리 계산해놓고
구간합을 구하라는 질문이 있을때마다 그 값을 꺼내쓰는 형태여야한다.
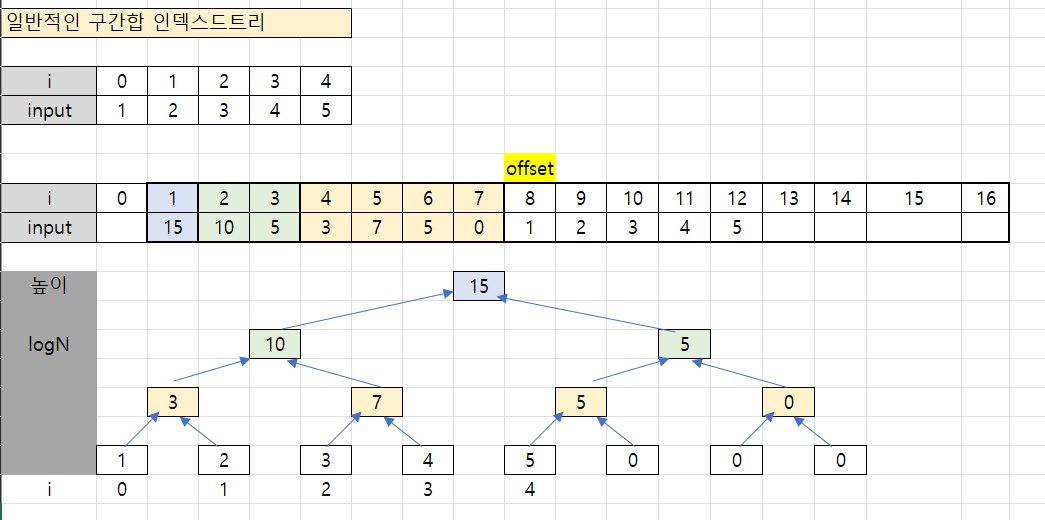
이러한 형태의 자료구조로는 인덱스드트리가 있다.
시간복잡도를 최소화하기 위해선 logN, 즉 이진구조의 자료구조가 필요하고
그러기 위해서 N보다 큰 최초의 2^N 크기의 데이터가 필요하다.
즉, N이 10일 경우엔 32.
N이 24일 경우엔 64.
N이 32일 경우에도 64.
N이 33일 경우엔 128 크기의 배열을 선언하고,
배열의 아래부분에는 입력받은 숫자를 그대로 넣고,
2로 나눠가면서 구간합을 미리 구해놓는 방식이다.
자세한 설명은 아래 링크를 참고.
참고 : 세그먼트 트리
https://www.acmicpc.net/blog/view/9
세그먼트 트리 (Segment Tree)
문제 배열 A가 있고, 여기서 다음과 같은 두 연산을 수행해야하는 문제를 생각해봅시다. 구간 l, r (l ≤ r)이 주어졌을 때, A[l] + A[l+1] + ... + A[r-1] + A[r]을 구해서 출력하기 i번째 수를 v로 바꾸기. A[i
www.acmicpc.net
2) 시간복잡도
인덱스드트리 값 수정시 시간복잡도 logN, 구간합 구할때 시간복잡도 logN으로
(M+K)*logN = 20000*log1000000 의 시간복잡도를 가져 여유있다.
(Java 기준 - 580ms)
3) 공간복잡도
문제 조건에서 2^63으로 숫자 범위를 정해주므로 int가 아닌 long으로 처리해야한다.
1) N 이 최대 100만이므로 넉넉잡게 400만으로 indexedTree를 선언해줘도 되고,
2) 공간을 아끼려면 for(nn = 1; nn<N; nn*=2); 를 통해 계산하면 2^21 = 2,097,152 으로 선언해도 된다.
400만으로 계산해도 어쨋든 nn을 기점으로 id를 계산해야하므로 nn*2 의 배열을 선언하는것을 추천.
400만 기준 4000000 * 8Bytes(long) = 약 30MBytes로 넉넉함.
4) 풀면서 놓쳤던점
특별히 없음.
5) 이 문제를 통해 얻어갈 것
인덱스드트리의 기본 개념 및 구현.
심화 내용을 원할 경우 Lazy propagation, Dynamic segment tree, Mo algorithm 등 공부.
C++ 코드 :
#include <cstdio>
using namespace std;
#define MAX_N 1000000
#define SZ_TR 2097152
typedef long long ll;
int N, M, K;
int OFFSET = 1;
ll array[MAX_N];
ll indexedTree[SZ_TR];
void init();
ll query(int from, int to);
void update(int idx, ll val);
int main()
{
int command; // 1이면 업데이트 / 2면 쿼리
ll x, y;
scanf("%d %d %d", &N, &M, &K);
for (int i = 0; i < N; i++)
{
scanf("%lld", &array[i]);
}
// 초기화
init();
for (int i = 0; i < M + K; i++)
{
scanf("%d %lld %lld", &command, &x, &y);
if (command == 1)
update(x - 1, y);
if (command == 2)
printf("%lld\n", query(x - 1, y - 1));
}
}
void init()
{
// 1. OFFSET 구하기 - N보다 크거나 같은, 최초의 2^k
while (OFFSET < N){
OFFSET *= 2;
}
// 2. OFFSET 기준으로 입력받은 값 그대로 입력
for (int i = 0; i < N; i++)
{
indexedTree[OFFSET + i] = array[i];
}
// 3. 입력받은 값 외에 값은 0으로 입력 (구간합에 포함되지 않기 위해)
// 테스트케이스가 여러번인 경우 특히 필요할 수 있으니 주의
for (int i = N; i < OFFSET; i++)
{
indexedTree[OFFSET + i] = 0;
}
// 구간합 데이터 만들어주기 - 밑에서부터 데이터를 쌓아올림. [1]이 root
for (int i = OFFSET - 1; i > 0; i--)
{
indexedTree[i] = indexedTree[i * 2] + indexedTree[i * 2 + 1];
}
}
// 구간합 쿼리
ll query(int from, int to)
{
ll res = 0;
from += OFFSET;
to += OFFSET;
while (from <= to)
{
// 왼쪽 id 가 홀수이면 값이 튀므로 현재 값을 더해주고 오른쪽으로 이동
// -> 짝수부터 시작해야하니까
if (from % 2 == 1)
{
res += indexedTree[from++];
}
// 오른쪽 id가 짝수면 값이 튀므로 현재 값을 더해주고 왼쪽으로 이동
// -> 홀수로 끝나야하니까
if (to % 2 == 0)
{
res += indexedTree[to--];
}
from /= 2;
to /= 2;
}
return res;
}
// 1) 해당 id 값 수정 2) 위로 올라가면서 구간합 갱신 -> logN의 시간복잡도
void update(int id, ll val)
{
// 1) 해당 id 값 수정
id += OFFSET;
indexedTree[id] = val;
// 2) 위로 올라가면서 구간합 갱신
while (id > 0)
{
id /= 2;
indexedTree[id] = indexedTree[id * 2] + indexedTree[id * 2 + 1];
}
return;
}
Java 코드 :
import java.io.*;
import java.util.*;
// 구간 합 구하기 백준 2042
public class Main {
static int N, M, K; // N 숫자 개수, M 변경 개수, K 질의 개수
static int offset; // 인덱스드트리의 기준이 되는 위치
static long[] indexedTree; // 인덱스드트리
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
// 1. 입력
// N, M, K 입력
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
// 인덱스드트리 크기 특정 및 선언 (offset은 N보다 크거나 같은, 최초의 2^N)
for (offset=1; offset<N; offset*=2);
indexedTree = new long[offset*2+2];
// 인덱스드트리에 데이터 입력 - 트리 하단에 1~N개 수의 최초 값을 입력
for (int i=0; i<N; i++) {
indexedTree[offset+i] = Long.parseLong(br.readLine());
}
// 2. 구간합 데이터 만들어줌 - 밑에서부터 데이터를 쌓아올림, [1] 이 root
for(int i=offset-1; i>=1; i--) {
indexedTree[i] = indexedTree[i*2]+indexedTree[i*2+1];
}
int size = M + K; // 변경과 쿼리의 합을 반복문 크기로 설정
for (int i=1; i<=size; i++) {
int type, x;
long y;
st = new StringTokenizer(br.readLine());
type = Integer.parseInt(st.nextToken()); // 1이면 edit, 2이면 쿼리
x = Integer.parseInt(st.nextToken()); // type=1 바꿀 수 / type=2 startId
y = Long.parseLong(st.nextToken()); // type=1 변경값 / type=2 endId
if (type==1) {
update(x-1,y);
}
else {
int endId;
endId = (int)y;
bw.write(String.valueOf(sum(x-1, endId-1))+"\n");
}
}
bw.flush();
bw.close();
br.close();
}
// 인덱스드트리 수정 1) 해당 id 값 수정 2) 위로 올라가면서 값 갱신 -> logN의 시간복잡도
static void update(int id, long value) {
int x = id + offset;
// 인덱스드트리 위치에 value로 값을 덮어쓰고
indexedTree[x] = value;
while(x>0) {
x /=2;
indexedTree[x] = indexedTree[x*2] + indexedTree[x * 2 + 1];
}
return;
}
// 인덱스드트리 합 구하기 위로 올라가면서 합 구하기
static long sum(int start, int end) {
int l = start + offset;
int r = end + offset;
long ret = 0;
while(l<=r) {
if ((l & 1) == 1) ret += indexedTree[l++]; // 왼쪽 id가 홀수이면 값이 튀므로 더해주고 l++ 해줌 (짝수부터 시작해야하니까)
if ((r & 1) == 0) ret += indexedTree[r--]; // 오른쪽 id가 짝수이면 값이 튀므로 더해주고 r-- 해줌 (홀수로 끝나야하니까)
l/=2; // 위로 올라가기
r/=2; // 위로 올라가기
}
return ret;
}
}'알고리즘 Algorithm > BOJ 백준 (초급~중급)' 카테고리의 다른 글
| [BOJ 백준] 가운데를 말해요(1655) C++, Java (0) | 2020.07.22 |
|---|---|
| [BOJ 백준] 달리기(2517) C++, Java (0) | 2020.07.21 |
| [BOJ 백준] 피보나치 수 2(2748) C++, Java (0) | 2020.07.14 |
| [BOJ 백준] 네트워크연결(1922) Java (0) | 2020.07.13 |
| [BOJ 백준] 암호만들기(1759) Java (0) | 2020.07.12 |